AIには数学知識が必要というので、
AIには数学知識が必要というので、
引き続き「はじめてのディープラーニング(我妻幸長[著])」を使用して学んでいきます。
1.数学基礎
| $$\sum$$ | 総和 | np.sum(<numpy配列>) |
| $$\sum{ab}$$ | 積の総和 | np.sum(<numpy配列>*<numpy配列>) |
| $$e^{x}$$ | ネイピア数の累乗 | np.exp(<値>) |
| $$log_ex$$ | 自然対数のlog | np.log(<値>) |
2.線形代数
(1) テンソル
「階数=添え字=次元数」かな?
| 階数 | 概念 | Python |
|---|---|---|
| 0 | スカラー | 値 |
| 1 | ベクトル | 配列 |
| 2 | 行列 | 2次元配列 |
| 3 | 3階のテンソル | 3次元配列 |
(2) テンソル形状変換
全要素数が同じであれば変換可能。
aryがa*b*c*dの1次元配列だとして、
| 階数 | 要素数 | 形状変換 |
|---|---|---|
| 1 | (abcd) | ary.reshape(a *b *c *d) |
| 4 | (a, b, c, d) | ary.reshape(a, b, c, d) |
| 2 | (abc, d) | ary.reshape(a *b *c, d) |
| 2 | (a, bcd) | ary.reshape(a, b *c *d) |
| 2 | (1, abcd) | ary.reshape(1, a*b*c*d) |
| 3 | (d, ac, b) | ary.reshape(d, a *c, b) |
(3) 積
(a) スカラー×行列
![]()
Pythonサンプル「3 * np.array([i for i in range(6)]).reshape(2,3)」
(b) 行列×行列(要素ごとの積)
Pythonサンプル「np.array([i for i in range(6)]).reshape(2,3) * np.array([ [0,1,2],[2,1,0] ])」
(c) 行列積
\(
AB=\left(\begin{array}{ccc}a_{11}& a_{12}& a_{13}\\a_{21}& a_{22}& a_{23}\end{array}\right)\left(\begin{array}{cc}b_{11}& b_{12}\\b_{21}& b_{22}\\b_{31}& b_{32}\end{array}\right)
\)
\(
\quad=\left(\begin{array}{cc}a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}& a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}
\\a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31}& a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}\end{array}\right)
\)
\(
\quad=\left(\begin{array}{cc}\sum{a_{1k}b_{k1}}& \sum{a_{1k}b_{k2}}\\\sum{a_{2k}b_{k1}}& \sum{a_{2k}b_{k2}}\end{array}\right)
\)
※処理後の形状は、「前行列の行×後行列の列」となる。(「2×3」「3×2」=「2×2」)
※対応する軸の要素数は同じである必要がある(「前行列の列の要素数」と「後行列の行の要素数」)
Pythonサンプル「np.dot(np.array([i for i in range(6)]).reshape(2,3), np.array([6-i for i in range(6)]).reshape(2,3).T)」
3.微分
微分とは「入力の変化量が出力に与えた影響の割合」であり、「出力÷入力」(変化割合)。
または導関数を得ること(導関数が割合や傾き、勾配のことなので上述と同じ意味)。
(1) 常微分
「\(x\)」を入力とし、「\(y\)」を出力とすると、「\(y\)」は「\(x\)」を”なんやかんや”した結果なので、“なんやかんや”を関数fと置くと、「\(y=f(x)\)」と書ける。
「\(x\)」から「\(x+α\)」に入力が変化した場合を考えると
・「\(x\)」に対する出力は「\(f(x)\)」
・「\(x+α\)」に対する出力は「\(f(x+α)\)」
・入力の変化量は「\((x+α)-x\)」
・出力の変化量は「\(f(x+α)-f(x)\)」
・変化の割合は「出力/入力」=「\(\frac{f(x+α)-f(x)}{(x+α)-x}=\frac{f(x+α)-f(x)}{α}\)」
・昔の人は入力の変化量は「\(α\)」ではなく「\(Δx\)」とお決めになったので、変化の割合は「\(\frac{f(x+Δx)-f(x)}{Δx}\)」
「\(Δx\)」を0に限りなく近づけた場合の変化の割合を「\(f'(x)\)」と書き、導関数と呼ぶ。
「\(f'(x)\)」は「\(\frac{d}{dx}f(x)\)」とも書き、「\(\frac{d}{dx}\)」は「xで微分する」という意味。※「\(f(x)\)」を「\(y\)」とした場合、「\(\frac{dy}{dx}\)」とも書く。
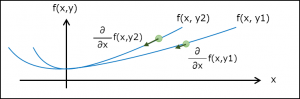
※あぁ勘違い
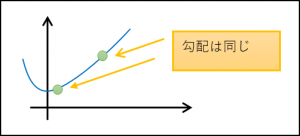
f(x)のどのx辺りにフォーカスするかで勾配は違う、f'(x)はどの辺の勾配なの?と思ってた。
実はどのx辺であっても勾配は同じとのこと。
「\(f(x)\)」を「\(x^2\)」とした場合の導関数を求めてみる。
\(
f'(x)=\frac{f(x+Δx)-f(x)}{Δx}=\frac{(x+Δx)^2-x^2}{Δx}
\)
\(\qquad
=\frac{(x^2+2xΔx+Δx^2)-x^2}{Δx}=\frac{2xΔx+Δx^2}{Δx}=2x+Δx
\)
「\(Δx\)」を限りなく0(つまり0)にすると
\(
2x+Δx = 2x
\)
よって、「\(x^2\)」の勾配はどの地点でも「\(2\)」といえる。
(2) 微分公式
覚えてしまおう
| 基本公式 | \(\frac{d}{dx}f(x)=rx^{r-1}\) ※\(f(x)=x^{r}\)の場合 |
|---|---|
| 関数の和 | \(\frac{d}{dx}(f(x)+g(x))=\frac{d}{dx}f(x)+\frac{d}{dx}g(x)\) |
| 関数の積 | \(\frac{d}{dx}(f(x)×g(x))=f(x)\frac{d}{dx}g(x)+g(x)\frac{d}{dx}f(x)\) |
| 定数 | \(\frac{d}{dx}k×f(x)=k\frac{d}{dx}f(x)\) |
| 累乗 | \(\frac{d}{dx}a^{x}=a^{x}loga\) |
| ネイピア数の累乗 | \(\frac{d}{dx}e^{x}=e^{x}\) ※\(log_{e}e=1\)のため |
| ネイピア数の負累乗 | \(\frac{d}{dx}e^{-x}=-e^{-x}\) |
| 自然対数 | \(\frac{d}{dx}logx=\frac{1}{x}\) |
| 出力の対数値を微分 | \(\frac{d}{dx}logy=\frac{y’}{y}\) ※\(y=f(x)、y’=f'(x)\) |
※「ネイピア数の負累乗」の導出
・分解・・・「\(y=e^{-x}\)」→「\(y=e^{u}、u=-x\)」
・微分・・・「\(\frac{d}{du}y=\frac{d}{du}e^{u}=e^{u}=e^{-x}\)」、「\(\frac{d}{dx}u=\frac{d}{dx}-x=-1\)」
・合成・・・「\(\frac{d}{dx}y=\frac{dy}{du}\frac{du}{dx}=e^{-x}×-1=-e^{-x}\)」
※「出力の対数値を微分」の導出
・\(\frac{d}{dx}logy=\frac{d}{dy}\frac{dy}{dx}logy=\frac{d}{dy}logy\frac{dy}{dx}=\frac{1}{y}y’=\frac{y’}{y}\)
(3) 連鎖律
出力が連鎖している場合、
「\(x → u → y\)」・・・「\(x → g(x) = u → f(u) = y\)」
※入力xが出力uに影響を与え、uが出力yに影響を与えている
並べて書くと
\(y=f(u)\)
\(u=g(x)\)
このように複数の関数の合成であらわされる関数を合成関数という。
例えば、「\(y=(x^{2}+1)^{3}\)」は「\(x^{2}+1\)」を「\(u\)」に置き換えると「\(y=u^{3}\)」となるので、合成関数といえる。
合成関数の導関数は各関数の積であらわすことができる
\(f'(x)=\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\)
(4) 偏微分
入力「x,y」、出力「z=f(x,y)」のように複数の変数を持つ関数(多変数関数)に対する、1つの変数のみによる微分を偏微分という。
偏微分により得られた導関数を偏導関数という。
※偏微分対象以外の変数は定数として扱う
\(\frac{∂}{∂x}f(x,y)=\lim\frac{f(x+Δx,y)-f(x,y)}{Δx}\) ※yが変化しておらず定数として扱える
例)「\(f(x,y)=3x^{2}+4xy+5y^{3}\)」を偏微分する
●xで偏微分
\(\frac{∂}{∂x}f(x,y)=3*2x^{(2-1)}+4*1x^{(1-1)}*y+5*0x^{(0-1)}*y^{3}\)
\(\hspace{3em}=6x+4y\)
●yで偏微分
\(\frac{∂}{∂y}f(x,y)=3x^{2}*0y^{(0-1)}+4x*1y^{(1-1)}+5*3y^{(3-1)}\)
\(\hspace{3em}=4x+15y^{2}\)
(5) 全微分
多変数関数に対する、各変数を考慮した微分を全微分という。
例)「\(z=f(x,y)\)」の全微分
\(dz=\frac{∂z}{∂x}dx+\frac{∂z}{∂y}dy\)
※「xの偏微分」×「xの微小変化量」+「yの偏微分」×「yの微小変化量」
dx,dyは微分のため0に限りなく近い値であるため、dzはzの勾配を表しているといえる。
上記例のように、全微分は偏微分から求めることができる。
一般式は「\(dz=\sum\frac{∂z}{∂x_{i}}dx_{i}\)」
(6) 多変数の連鎖律
(a) 入力1つ
| \(z=f(u, v)\) \(u=g(x)\) \(v=h(x)\) |
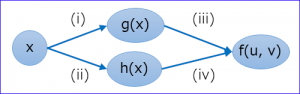 |
| ①全微分の公式から | \(dz=\frac{∂z}{∂u}du+\frac{∂z}{∂v}dv\) |
| ②両辺をdxで割る | \(\frac{dz}{dx}=\frac{∂z}{∂u}\frac{du}{dx}+\frac{∂z}{∂v}\frac{dv}{dx}\) |
| ③一般式 | \(\frac{dz}{dx}=\sum\frac{∂z}{∂u_{i}}\frac{du_{i}}{dx}\) |
「\(f(u, v)\)」の勾配は
「出力側(u,v→z)の偏微分」×「入力側(x→u,v)の微分」の総和
図の番号でいうと、「(i)×(iii)+(ii)×(iv)」となる
(b) 入力2つ
| \(z=f(u, v)\) \(u=g(x, y)\) \(v=h(x, y)\) |
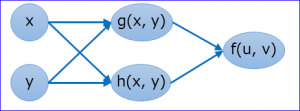 |
| ①入力1つの場合の一般式から | \(\frac{∂z}{∂x}=\frac{∂z}{∂u}\frac{∂u}{∂x}+\frac{∂z}{∂v}\frac{∂v}{∂x}\) \(\frac{∂z}{∂y}=\frac{∂z}{∂u}\frac{∂u}{∂y}+\frac{∂z}{∂v}\frac{∂v}{∂y}\) |
| ②一般式 | \(\frac{∂z}{∂x_{i}}=\sum\frac{∂z}{∂u_{j}}\frac{∂u_{j}}{∂x_{i}}\) |
ただ「(a) 入力1つ」を複数入力としてまとめなおしただけ。
「入力側(x,y→u,v)の微分」は他方の入力の影響を無視させるため偏微分になっている。
(7) 正規分布
公式をおさらい
| 平均 | \(μ=\frac{\sum_{k=0}^{n}x_{k}}{n}\) |
|---|---|
| 標準偏差 | \(σ=\sqrt{(\frac{\sum_{k=0}^{n}(x_{k}-μ)^{2}}{n})}\) |
| 確率密度関数(正規分布) | \(y=\frac{1}{\sqrt{2πσ^{2}}}exp(-\frac{(x-μ)^{2}}{2σ^{2}})\) |