いままで考えないようにしてた
いままで考えないようにしてた
探索アルゴリズム
(1) 線形探索
端から順番に調べる方法。
●平均比較回数・・・N/2(平均だから半分)
●最大比較回数・・・N(目的要素が最後だった場合)
※N:要素数
(2) 2分探索
半分でグループ分けし該当グループを残していく方法。
要素が整列されている必要がある。
●平均比較回数・・・log2N(端数切捨て)(半分に分割する回数)
●最大比較回数・・・平均比較回数+1(Nが奇数の場合、+1)
整列アルゴリズム
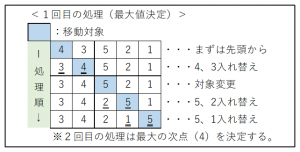
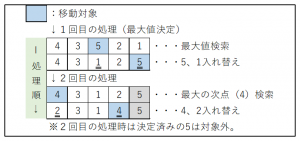
(1) バブルソート
最大値(または最小値)から決定していく方法。
(1回目は最大値を決定し、2回目は最大値の次点を決定する)
先頭から順に要素を比較して入れ替えながら最大値を右に移動していく。
(2) 選択ソート
最大値(または最小値)から決定していく方法。
配列全体(2回目はN-1)から最大値を抽出し、最後尾要素を入れ替える。
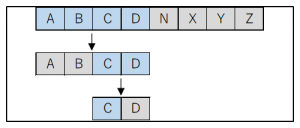
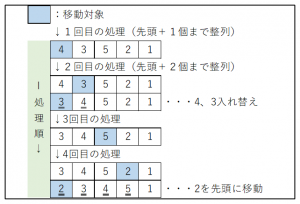
(3) 挿入ソート
先頭から順に整列していく方法。
X回目の処理では先頭からX個目の要素が整列された状態になる。
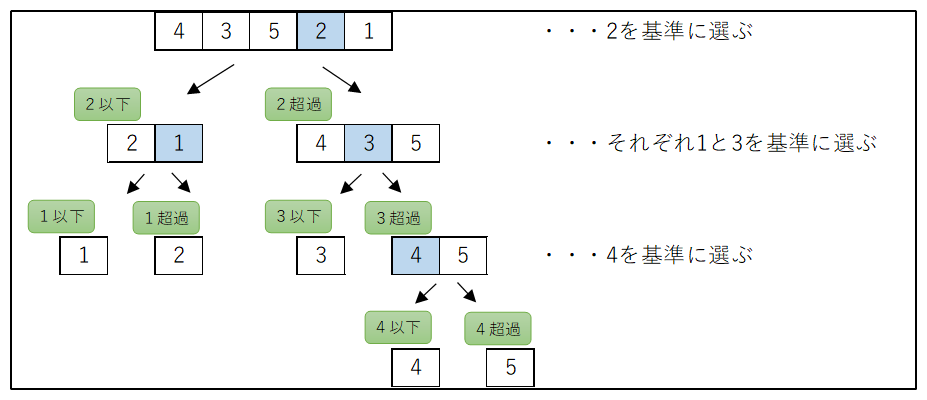
(4) クイックソート
任意の要素を基準として大、小2つのグループに分ける方法。
グループの要素数が1になるまで、繰り返す。
(5) マージソート
一旦、要素をバラバラに分割して、マージする際に整列する方法。
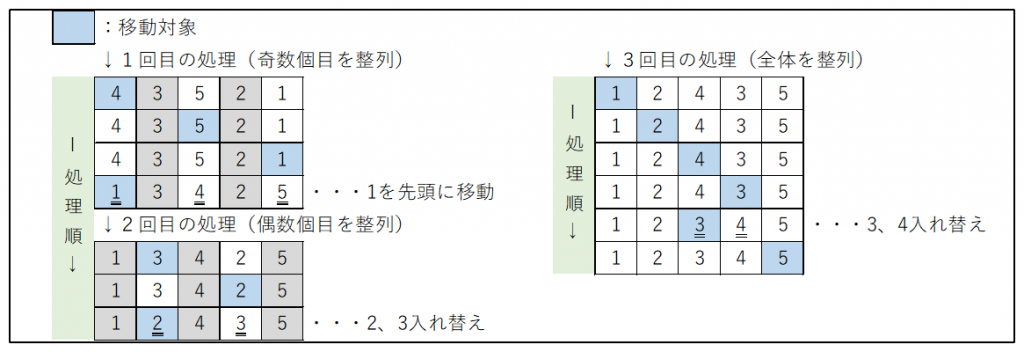
(6) シェルソート
挿入ソートを改良して高速化した方法。
整列対象を一定間隔(奇数個目など)の要素に分けて処理する。
要素の移動数を減らすことができる。
※移動数の比較
図の整列対象「43521」で比較する。
挿入ソート・・・11要素(=2回目の処理「2要素」+4回目の処理「4要素」+5回目の処理「5要素」)
シェルソート・・・7要素(=1回目の処理「3要素」+2回目の処理「2要素」+3回目の処理「2要素」)
(7) ヒープソート
ヒープのデータ構造の場合、根が最大となる。
根の取り外しとヒープの再構築を繰り返すと、整列することができる。
文字列探索アルゴリズム
(1) 力まかせ探索法
検索文字列の一致状態にかかわらず、被検索文字列を1つずつずらして探索する方法。
(2) ボイヤー・ムーア法(BM法)
検索文字列を比較した最後の被検索文字列の文字によって移動先が変化する方法。