論理演算はできなきゃ困る、表記法は使うことない
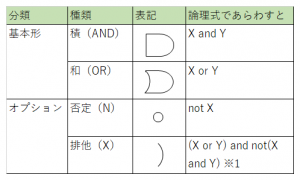
論理演算
表記方法はいくつかあるようなので注意。以下は一例。
※1．XORの例。XANDは無い（あったら常にFalseだろうか）。
●論理一致素子
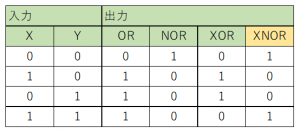
これは「否定排他的論理和（XNOR）」のこと。XORのNOT。
入力が同じ場合（True同士、False同士）にTrueになるので、同値や等価とも呼ばれる。
表で確認
※ド・モルガンの法則とか、半加算器、全加算器は省略。
表記法
(1) BNF
構文定義の一手法。正規表現っぽい。
e.g.
「<数字>::=0|1|2|3|4|5|6|7|8|9」
「<数字列>::=<数字>|<数字列><数字>」（単独の数字または繰り返し）
「<小数>::=[<数字列>]<.><数字列>」（整数部は省略可能）
(2) 逆ポーランド法
数式を機械的に解釈する表記法
「<数値><数値><演算子>」で表す。
e.g.「元の式 e = a – b ÷ (c + d)」
計算順序どおりに全部括弧をつけると「e = (a – (b ÷ (c + d)))」
逆ポーランド法で表記すると「eabcd+÷-=」となる。
(3) ポーランド法
逆ポーランド法の逆に表記する。
「<演算子><数値><数値>」で表す。
e.g.「元の式 e = a – b ÷ (c + d)」
ポーランド法で表記すると「=e-a÷b+cd」となる。