画像認識の技術です。
画像認識の技術です。
引き続き「はじめてのディープラーニング(我妻幸長[著])」を使用して学んでいきます。
1.畳み込みニューラルネットワーク(CNN)とは
画像認識を得意とするネットワーク。画像を入力とした分類問題をよく扱う。
(1) CNNの構成
※逆伝播は上図の逆(全結合層→プーリング層→畳み込み層)で行われる。
※各層の学習対象パラメータは以下。
| 層 | 学習対象パラメータ |
|---|---|
| 畳み込み層 | フィルタ、バイアス |
| プーリング層 | なし |
| 全結合層 | 重み、バイアス |
(2) 各種処理の概要
| 畳み込み | 特徴を強調する(局所性を利用して特徴を検出する) |
|---|---|
| プーリング | 特徴を生かしたまま位置を補正する(位置情報を希薄にする→対象の位置に捉われない判定を可能にする) |
| パディング | 画像の定数での拡張。畳み込みやプーリング時で縮小された画像を拡張する。 |
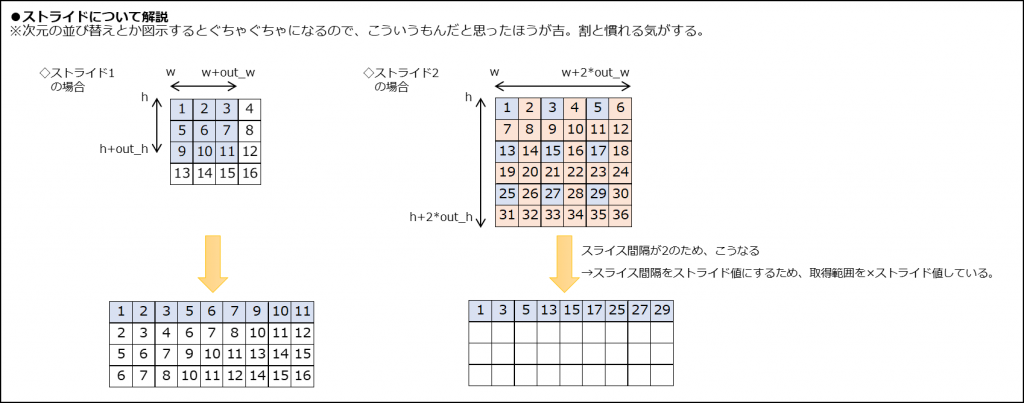
| ストライド | 畳み込み時の移動間隔。間隔が大きいと雑に畳み込む。画像があまりにも大きい場合に2以上にするが、通常は1。 |
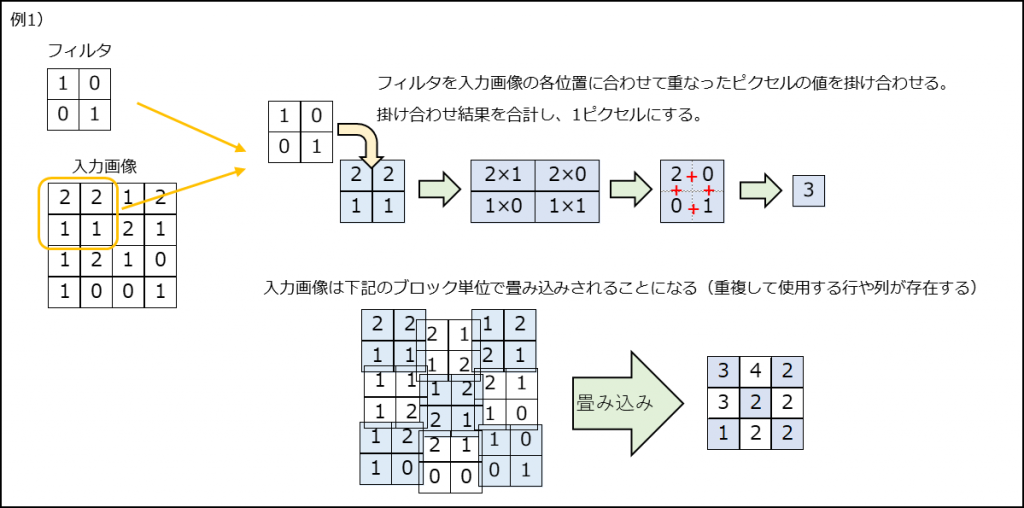
(3) 畳み込み
フィルタを画像に適用して、特徴を強調した画像を作成することを畳み込みという。
画像は色別のチャンネルを持っているので、フィルタも対応したチャンネルを持ち、それぞれのチャンネルで畳み込みを行う。
畳み込み後はチャンネル別の画像はピクセルを合計し、1つの画像にする。
※チャンネル・・・モノクロなら1つ。RGB画像なら3つ。
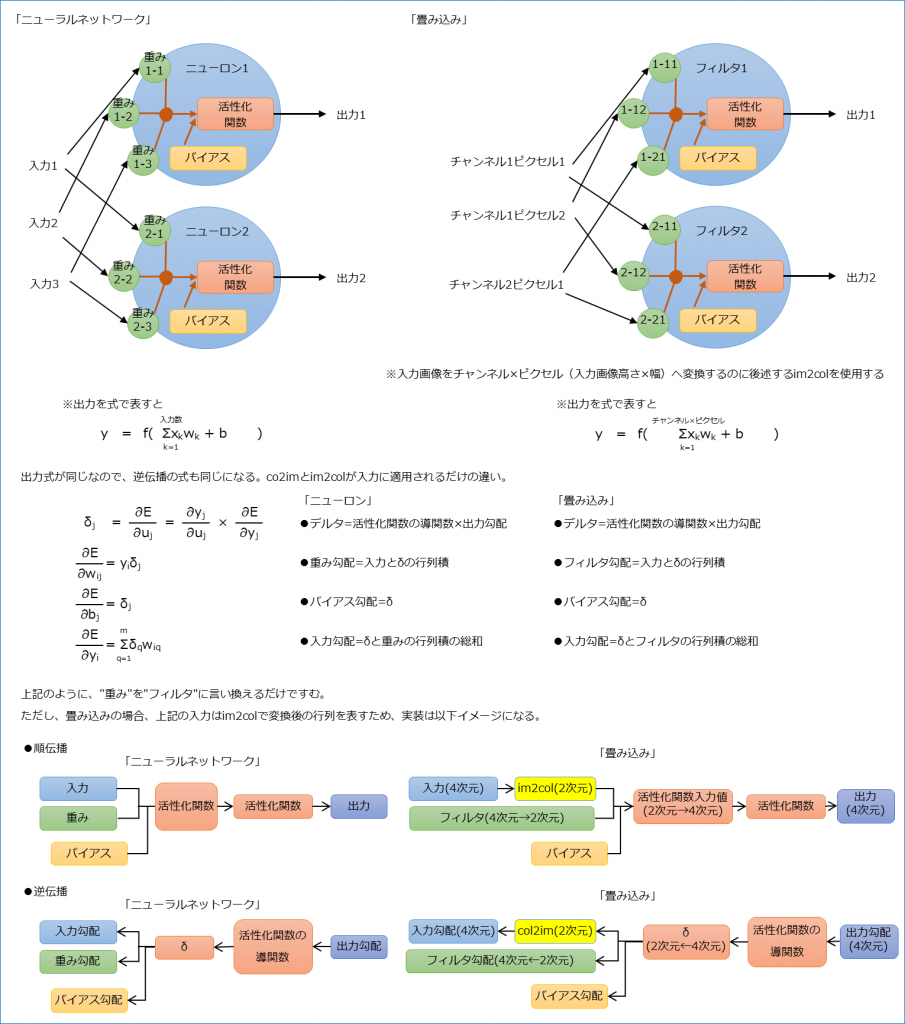
畳み込み層の出力はニューロンと同じように畳み込み結果にバイアスを足し、活性化関数を通したものとなる。
また、1つのフィルタが1つのニューロンに相当し、出力数はフィルタ数と同じになる。
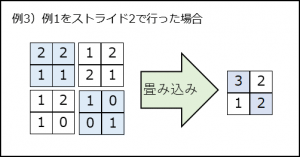
畳み込み時の移動間隔をストライドという。
上記例1)のストライドは1。大きすぎる画像の場合は2以上にすることもあるが、通常は1。
出力画像のサイズの公式(畳み込み後のサイズ)
・入力画像のサイズ \(I_{h}×I_{w}\)
・フィルタのサイズ \(F_{h}×F_{w}\)
・パディングの幅 \(D\)
・ストライドの値 \(S\)
・出力画像のサイズ \(O_{h}×O_{w}\)
とすると、
\(O_{h}=\frac{I_{h}-F_{h}+2D}{S}+1\)
\(O_{w}=\frac{I_{w}-F_{w}+2D}{S}+1\)
※高さ\(O_{h}\)の式についてひも解く(\(O_{w}\)も同じ考え方)
- ストライドが1の場合の畳み込み時の移動回数は「\(I_{h}-F_{h}\)」。
※\(I_{h}\)が6、\(F_{h}\)が2なら、4回移動できる。- ストライドがSの場合の畳み込み時の移動回数は「\(\frac{I_{h}-F_{h}}{S}\)」。
※\(I_{h}\)が6、\(F_{h}\)が2なら、2回移動できる。- 畳み込みする回数は「移動回数+初期位置での1回」なので「\(\frac{I_{h}-F_{h}}{S}+1\)」。
- パディングは両側に行うので、入力画像に2Dを足す「\(\frac{I_{h}+2D-F_{h}}{S}+1\)」。
- 出力画像のサイズは畳み込みをした回数と同じになるので、4.が出力画像サイズとなる。
※畳み込みをするとそのフィルタ範囲が1ピクセルになるので、回数は出力画像サイズと等しい。
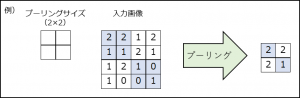
(4) プーリング
入力画像に対し、特定サイズの領域毎に代表値を選定し、新しい画像を作ること。
領域内の最大値を代表値とする方法をMAXプーリングといい、平均値を代表値とする方法を平均プーリングという。
画像の特徴を残したままサイズを小さくすることになるので、画像が粗くなり、対象の位置の変化に疎くなり、結果が安定する。
(5) パディング
入力画像を取り囲むようにピクセルを配置すること。
畳み込み層やプーリング層で行われる。
畳み込み層やプーリング層で小さくされた画像を拡張することで画像サイズが変わらないようにしたり、畳み込み回数の少ない画像端の特徴を取り入れやすくするために使用される。
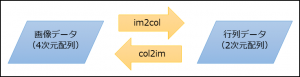
2.im2colとcol2imとは
畳み込み層とプーリング層を実装しやすくし、実行速度を早くするために用いられるアルゴリズム。
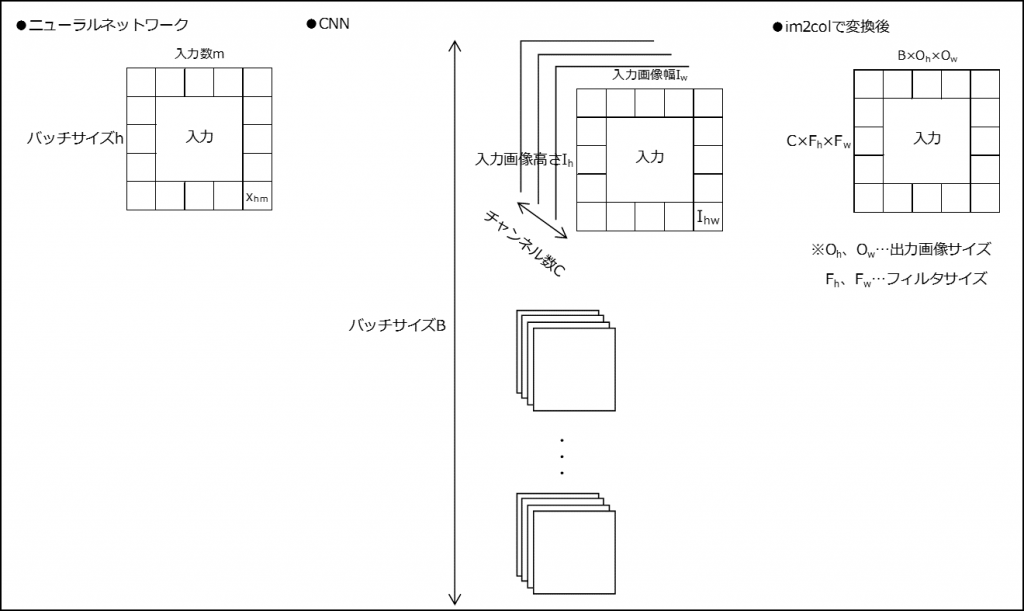
画像データは画像高さ、画像幅、チャンネル数、バッチサイズで4次元になってしまい、扱いづらい。
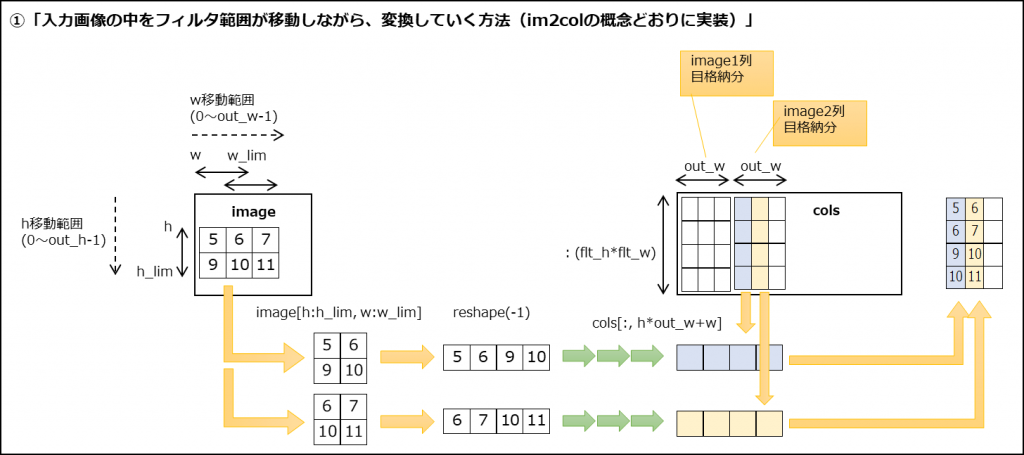
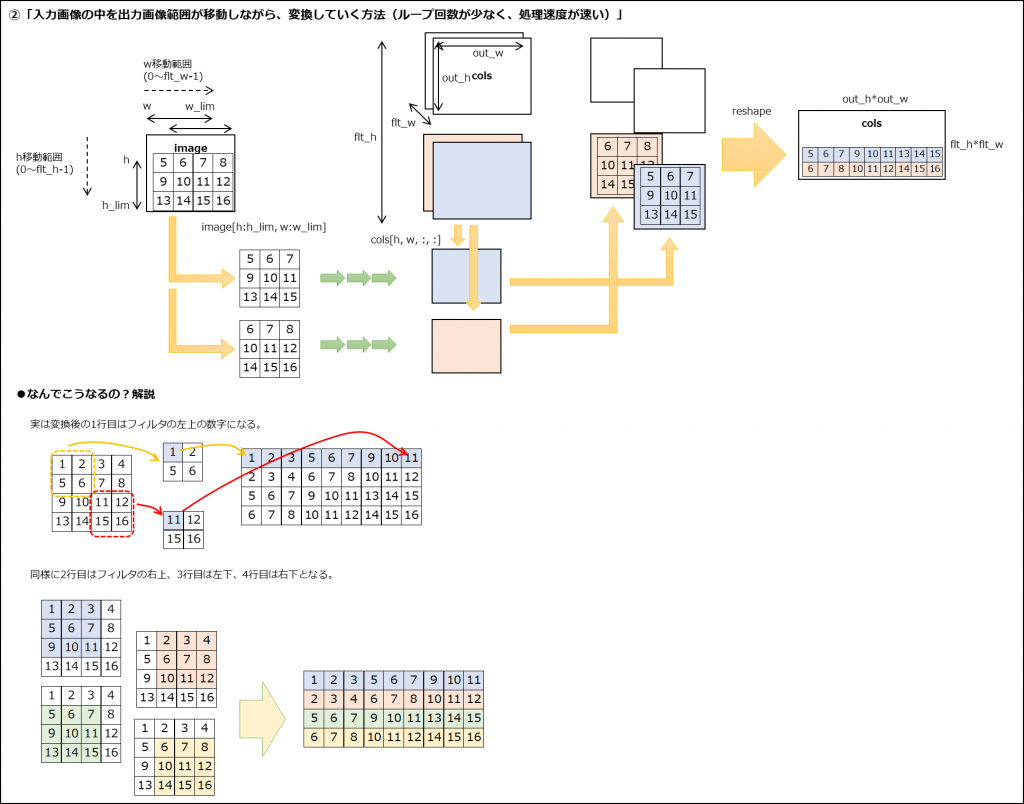
(1) im2colのアルゴリズム
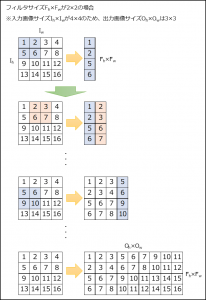
①入力画像\(I_{h}×I_{w}\)を\((F_{h}×F_{w})×(O_{h}×O_{w})\)に変換
※変換範囲(フィルタサイズ)の移動の仕方は畳み込みと同じ。
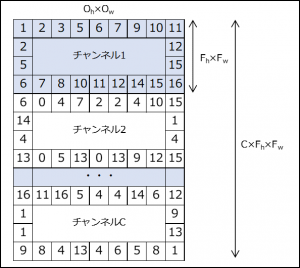
②チャンネル数分「①」を繰り返し、結果を最終行に追加する。
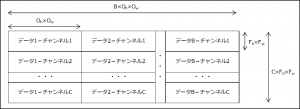
③バッチサイズ分「②」を繰り返し、結果を最終列に追加する。
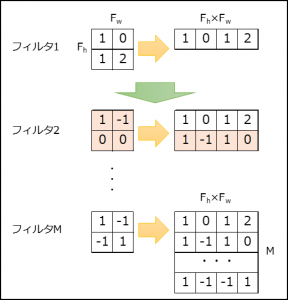
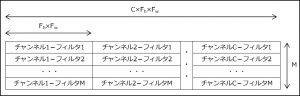
④フィルタ(サイズ\(F_{h}×F_{w}\)、個数\(M\))を\(M×(F_{h}×F_{w})\)に変換
⑤チャンネル数分「④」を繰り返し、結果を最終列に追加する。
以上
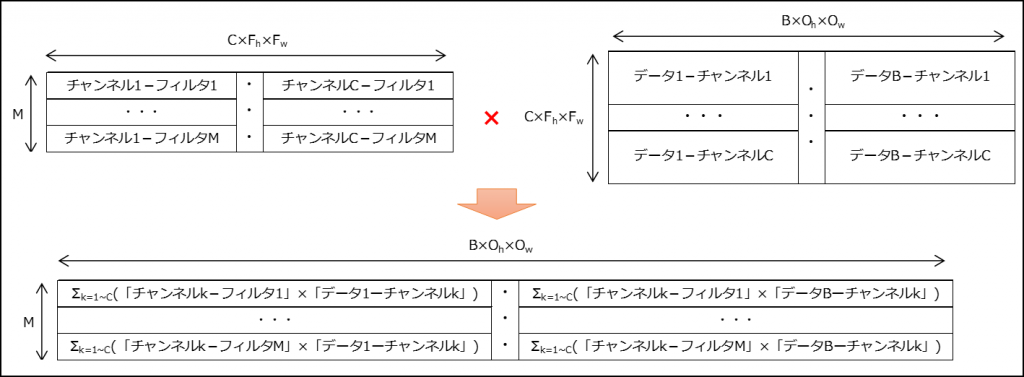
im2colの変換により、畳み込みはフィルタ「\(M×(C×F_{h}×F_{w})\)」と「\((C×F_{h}×F_{w})×(B×O_{h}×O_{w})\)」の行列積で求められるようになる。
結果は「\(M×(B×O_{h}×O_{w})\)」となる。
(2) col2imのアルゴリズム
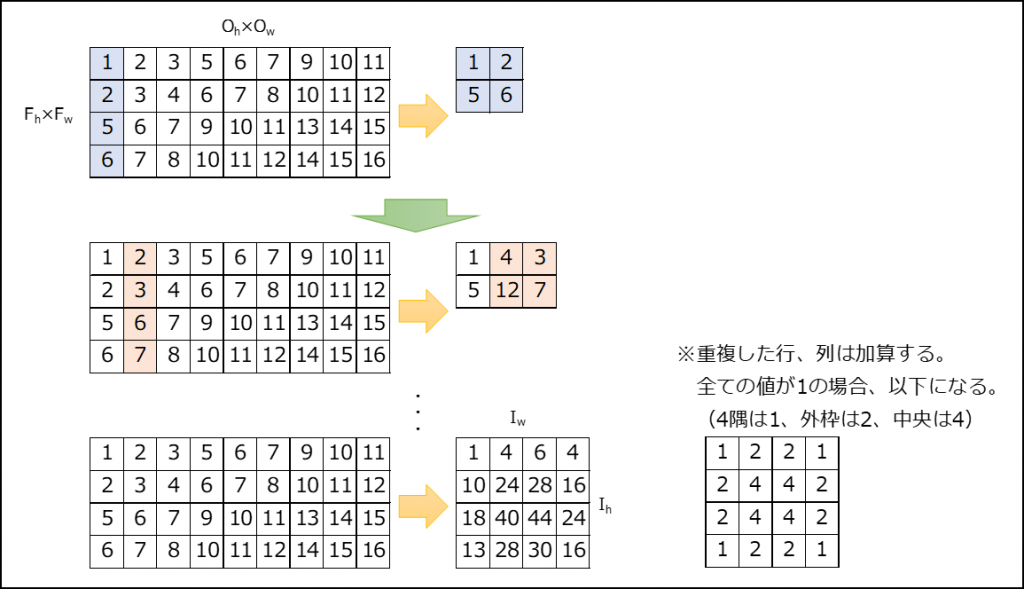
①画像\((F_{h}×F_{w})×(O_{h}×O_{w})\)を\(I_{h}×I_{w}\)に変換
②チャンネル数分「①」を繰り返し、結果を別の次元に追加する。「\((C, I_{w}, I_{h})\)」
③チャンネル数分「②」を繰り返し、結果を別の次元に追加する。「\((B, C, I_{w}, I_{h})\)」
3.実装に際して
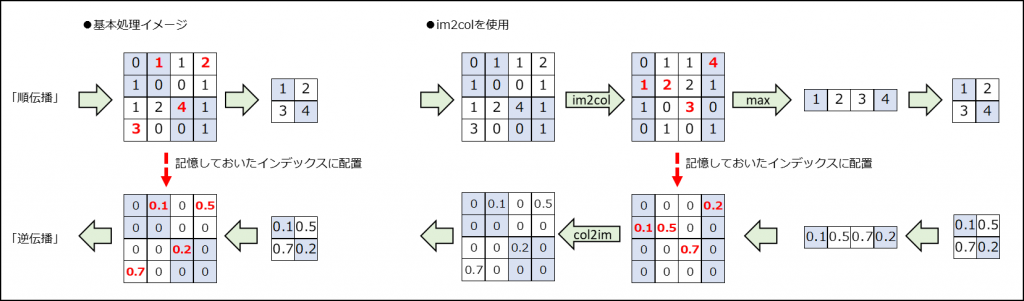
(1) im2colの処理イメージ
※処理イメージだけ見ても何のことかわからないと思います。書籍のサンプルコードと見比べてみてください。(書籍の7.2.3、7.2.4)
(2) 畳み込み層の実装(書籍の7.3)
im2colとcol2imを使用することで、畳み込みのフィルタはニューラルネットワークの重みと同じように扱うことができる。
(3) プーリング層の実装(書籍の7.4)
im2colとcol2imを利用することで簡単に処理ができる。
順伝播でプーリングサイズで1つの値しか出力していないため、
逆伝播の際は順伝播で出力に使用したインデックスに対応した勾配のみが入力勾配になる。
(4) CNNの実装
書籍7.7のCNNに追加して、入力画像のサイズを拡張して位置をランダムに散らしてみました。
(フィルタ数は20、全結合層中間層のニューロン数は400にしてあります)