［ディープラーニング入門］④バックプロパゲーション

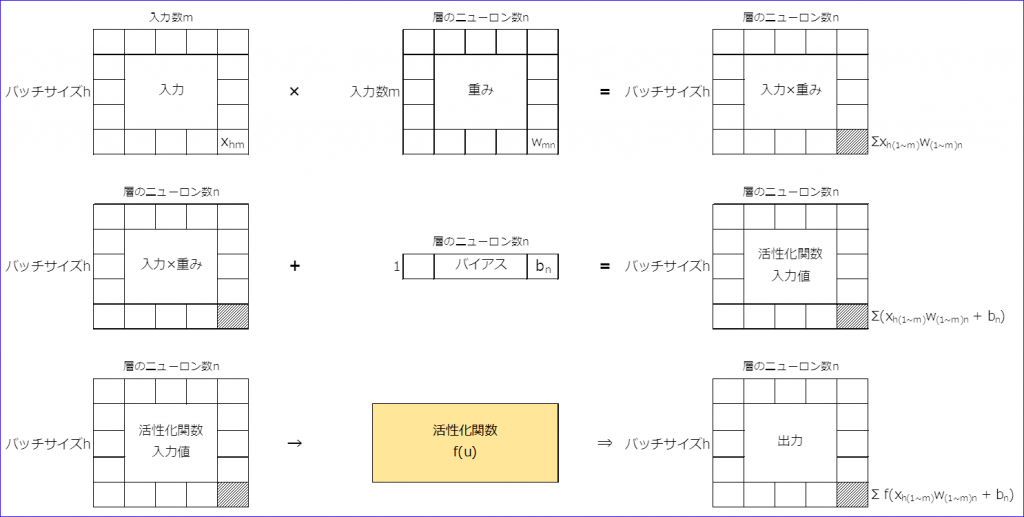
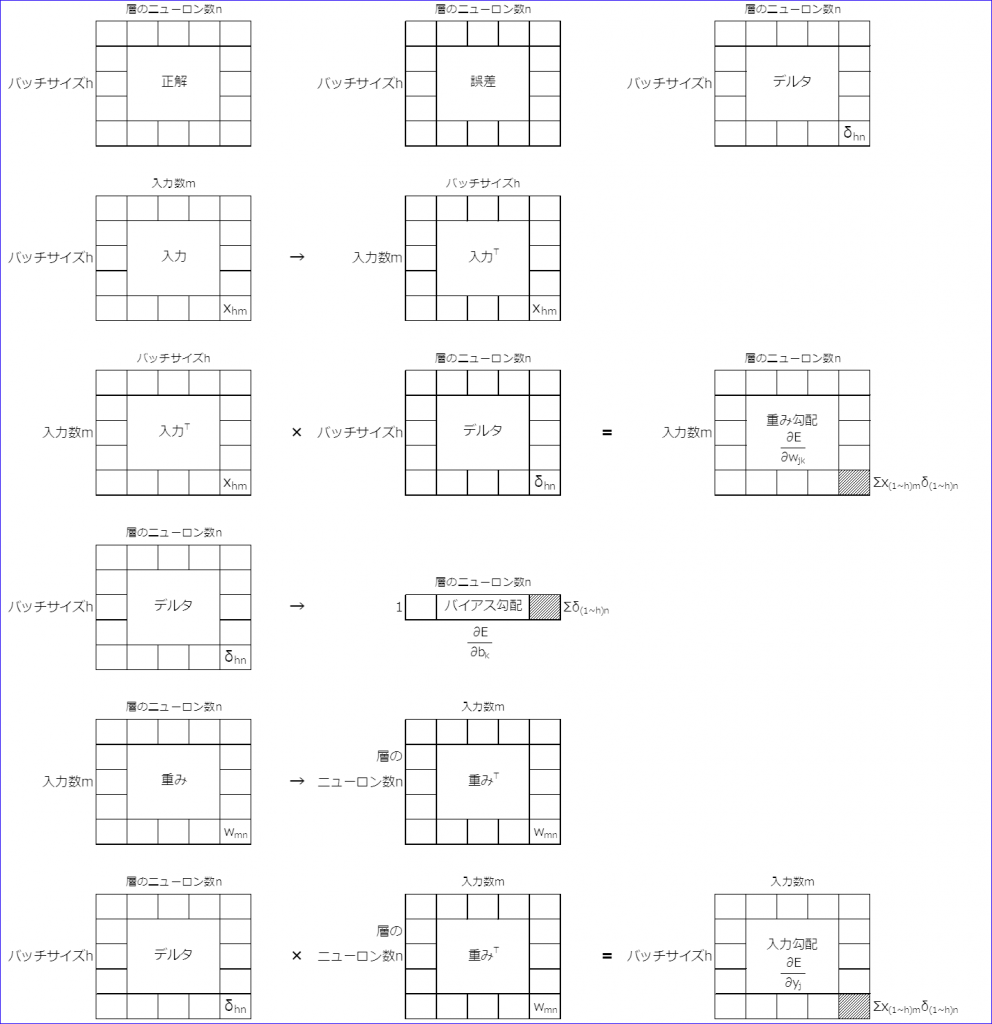
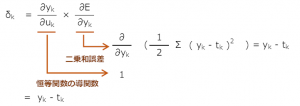ネットワークが学習する仕組み。

引き続き「はじめてのディープラーニング（我妻幸長[著]）」を使用して学んでいきます。

１．概念

バックプロパゲーション（誤差逆伝播法）とは

学習アルゴリズムの１つ。
出力と正解の誤差から遡って（出力層から入力層に向けて）順番に重みとバイアスを更新していく方法。

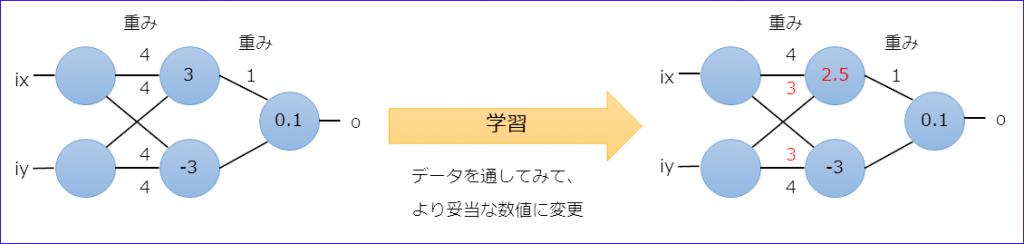
学習って何？

重みとバイアスをよりよくすること（最適化）。

神経細胞ネットワークだと出力の高いニューロン間が強化される「ヘッブ則」と正解との差で調整する「デルタ則」があるそうだ。
バックプロパゲーションは誤差を使う、つまり正解が存在するので「デルタ則」に基づいた方法ということだろうか。

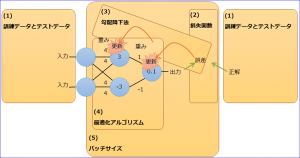
バックプロパゲーションの５つの要素

(1) 訓練データとテストデータ

「訓練データ」は学習で使用するデータ、「テストデータ」は学習結果を評価するために使用するデータ。
データを用意したら、一部をテストデータにして、残りを訓練データにするみたい。普通は訓練データの方が多いとのこと。
誤差が必要なので、各データは入力情報と正解情報がセットになる。

(2) 損失関数

誤差を定義する関数。
代表的なものとして、出力と正解の差を誤差とする「二乗和誤差」と、分類問題でよく使用される「交差エントロピー誤差」がある。

二乗和誤差	\(E=\frac{1}{2}\sum(y_{k}-t_{k})^{2}\)
交差エントロピー誤差	\(E=-\sum t_{k}log(y_{k})\)

※記号の意味・・・E:誤差、k:出力のニューロン、y:出力値、t:正解値

交差エントロピー誤差の\(-log(y_{k})\)は\(y_{k}\)が1に近づけば0に近づくことになるのでone-hot表現に適している。
またlogのため正解との乖離が大きい場合は誤差も大きくなり学習速度が速くなる利点がある。

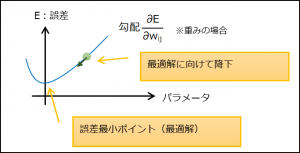
(3) 勾配降下法

パラメータ（重み、バイアス）の誤差に対する勾配を用いて誤差を最小にする方法。

(4) 最適化アルゴリズム

最適化（誤差修正）の際の更新量を決める方法。
代表的なものに以下の種類がある。

●確率的勾配降下法（SGD)
更新ごとに使用するデータを訓練用データからランダムにサンプリングする方法。

メリット	局所最適解に囚われにくい。更新式がシンプル。
デメリット	更新量の調整が柔軟にできない。
更新式	※η：学習係数 \(w←w-η\frac{∂E}{∂w}\) \(b←b-η\frac{∂E}{∂b}\)

●Momentum
確率的勾配降下法に慣性を足した方法。前回の更新量の影響を受ける。

メリット	急激な更新を行わない。
デメリット	設定に必要な定数が２つになり、調整が難しくなる。
更新式	※η：学習係数、α：慣性係数、Δw/Δb：前回更新量 \(w←w-η\frac{∂E}{∂w}+αΔw\) \(b←b-η\frac{∂E}{∂b}+αΔb\)

●AdaGrad
学習が進むと、学習量が小さくなる方法。

メリット	効率のいい学習が可能。
デメリット	学習が進むと更新量がほぼ0になり、最適化が進まなくなる。
更新式	※η：学習係数 \(h_{w}←h_{w}+(\frac{∂E}{∂w})^{2}\) \(h_{b}←h_{b}+(\frac{∂E}{∂b})^{2}\) \(w←w-η\frac{1}{\sqrt{h_{w}}}\frac{∂E}{∂w}\) \(b←b-η\frac{1}{\sqrt{h_{b}}}\frac{∂E}{∂b}\)

●RMSProp
AdaGradに「忘れ」を追加した方法。更新量を抑えていた変数を一定割合で減少させる。

メリット	AdaGradの弱点を克服。
更新式	※η：学習係数、ρ：忘れ係数 \(h_{w}←ρh_{w}+(1-ρ)(\frac{∂E}{∂w})^{2}\) \(h_{b}←ρh_{b}+(1-ρ)(\frac{∂E}{∂b})^{2}\) \(w←w-η\frac{1}{\sqrt{h_{w}}}\frac{∂E}{∂w}\) \(b←b-η\frac{1}{\sqrt{h_{b}}}\frac{∂E}{∂b}\)

●Adam
いいとこどりの方法。

メリット	他の方法より高い性能を発揮することが多い。
デメリット	複雑。
更新式	※省略

(5) バッチサイズ

更新を行う間隔（データ数）。いくつかの訓練データで誤差を出してまとめて更新するので、バッチサイズ内は未学習のまま誤差を出すことになる。

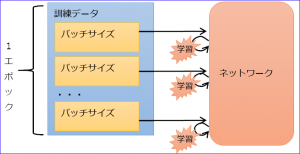
また、訓練データすべてを学習することを１エポックという。
バッチサイズにより３種類に分かれる。

学習タイプ	バッチサイズ	メリット	デメリット
バッチ学習	全訓練データ数	学習が高速	局所最適解に囚われやすい
オンライン学習	1	安定性に欠ける	局所最適解に囚われにくい
ミニバッチ学習	数個	やや安定性あり	局所最適解にやや囚われにくい

２．勾配の導出

(1) 概要

※図中で使用する添え字とニューロン数を表す記号

層	添え字	ニューロン数
入力層	i	l
中間層	j	m
出力層	k	n

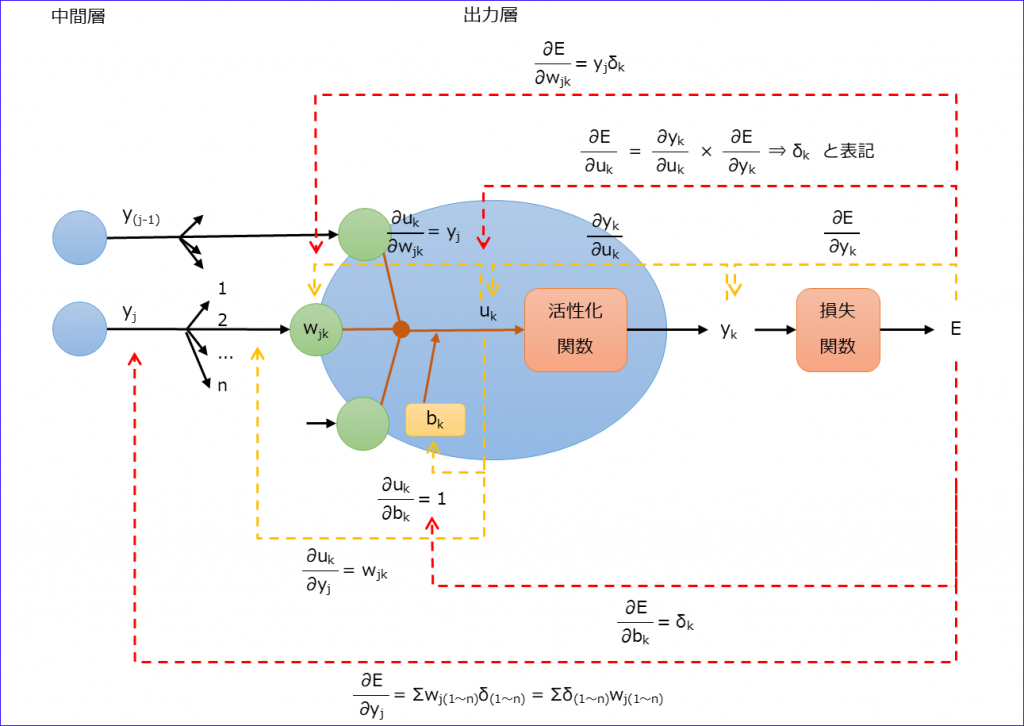
●出力層を考える

それぞれのポイントで入力に対する結果の割合を求め（黄線）、最終的に各入力値の誤差に対する割合を求める（赤線）。

※記号が多すぎてわかりづらいので、記号を減らす意味で以下のように記載しています。
\(\quad\sum_{r=1}^{n}δ_{r}w_{jr}=\sumδ_{(1～n)}w_{j(1～n)}\)

◆まとめると

\(δ_{k}=\frac{∂E}{∂u_{k}}=\frac{∂y_{k}}{∂u_{k}}\frac{∂E}{∂y_{k}}\)
\(\frac{∂E}{∂w_{jk}}=y_{j}δ_{k}\)
\(\frac{∂E}{∂b_{k}}=δ_{k}\)
\(\frac{∂E}{∂y_{j}}=\sum_{r=1}^{n}δ_{r}w_{jr}\)

●中間層は出力層の記号が変わるだけ

\(δ_{j}=\frac{∂E}{∂u_{j}}=\frac{∂y_{j}}{∂u_{j}}\frac{∂E}{∂y_{j}}\)
\(\frac{∂E}{∂w_{ij}}=y_{i}δ_{j}\)
\(\frac{∂E}{∂b_{j}}=δ_{j}\)
\(\frac{∂E}{∂y_{i}}=\sum_{q=1}^{m}δ_{q}w_{iq}\)

(2) 損失関数・活性化関数を適用

損失関数・活性化関数を決定した場合の、上記で求めた式の変形を行う。
※各層のδを求めれば、他の勾配は求まるので、δだけ式の変形を行う。

(a) 回帰問題を想定

使用する関数は以下とする
損失関数：二乗和誤差
活性化関数（中間層）：シグモイド関数
活性化関数（出力層）：恒等関数

出力層の\(δ_{k}\)

中間層の\(δ_{j}\)

(b) 分類問題を想定

使用する関数は以下とする
損失関数：交差エントロピー誤差
活性化関数（中間層）：シグモイド関数
活性化関数（出力層）：ソフトマックス関数