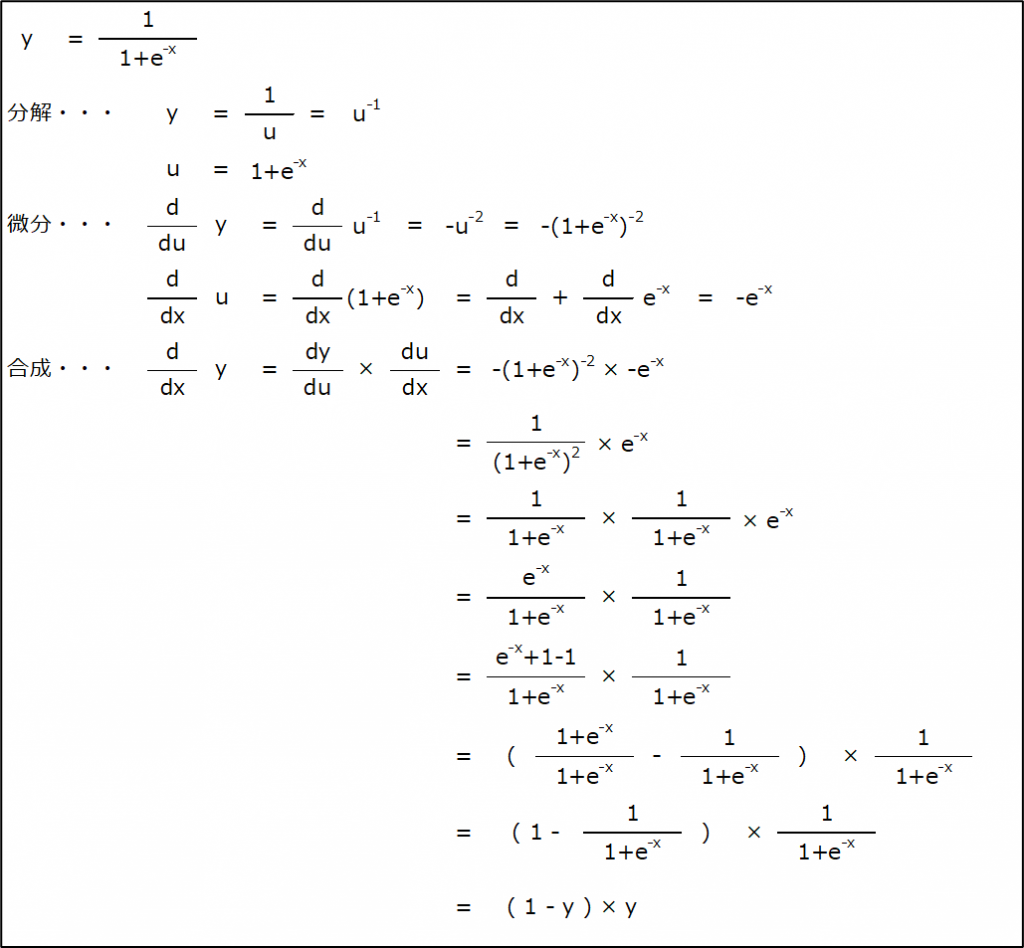［ディープラーニング入門］③ニューラルネットワーク

いよいよ、ディープラーニングの基礎に入っていきます。

引き続き「はじめてのディープラーニング（我妻幸長[著]）」を使用して学んでいきます。

１．モデル

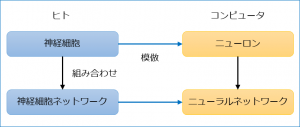
ニューロンとニューラルネットワークのモデルを示して説明をまとめていきます。

最初にニューラルネットワークのもとになった神経細胞ネットワークとの関係性から。

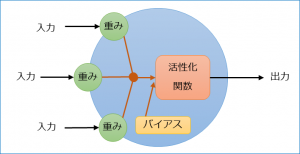
(1) ニューロンのモデル

●ニューロンは複数の入力を受け取る
●入力に対応した重みが存在し、入力に掛け合わせて重要度をコントロールする（神経細胞でいうところの伝達効率）
●ニューロンはバイアスを定数で持ち、ニューロン自身の重要度をコントロールする（いわば感度。感度がいいと影響を与えやすい）
●重みを掛けた入力とバイアスが活性化関数に渡され、その結果がそのニューロンの出力となる（※1）

※1．
入力をx、重みをw、バイアスをb、入力数をnとすると、活性化関数に入力する値uは
\(u=\sum_{k=0}^{n}(x_{k}w_{k})+b\)
となる（入力と重みを掛けたものの総和にバイアスを足した値）。
出力をy、活性化関数をf(u)とすると
\(y=f(u)=f(\sum_{k=0}^{n}x_{k}w_{k})+b)\)
となる。

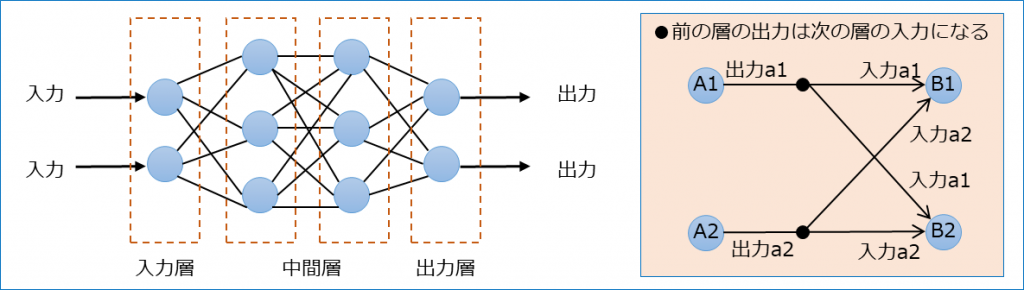
(2) ニューラルネットワークのモデル

●ニューロンを層上に並べる。
●各ニューロンの出力は次の層のすべてのニューロンに入力として伝達される。
●入力を受け取る層を入力層、最終的な出力を行う層を出力層、入力層と出力層の間の層を中間層（隠れ層）という。
●入力→出力の流れを順伝播（フォワードプロパゲーション）、出力→入力の流れを逆伝播（バックプロパゲーション）という。
●逆伝播はネットーワークを学習させるときに行われる。
●１つの層における、活性化関数入力値uと出力yを数式であらわす。（※1）

※1．

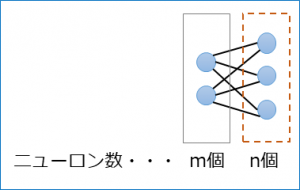
その層のニューロン数をn個とすると、uとyはn個存在するので、ベクトルとなり、以下のようにあらわす。
\((u_{1},u_{2},…,u_{n})=\vec{u}\)
\((y_{1},y_{2},…,y_{n})=\vec{y}\)
その層の１つ前のニューロン数をm個とすると\(\vec{u}\)と\(\vec{y}\)は前述のニューロンのモデルから以下のようにあらわせる。
\(\vec{u}=(\sum_{k=0}^{m}(x_{k}w_{k1})+b_{1}, \sum(x_{k}w_{k2})+b_{2}, … , \sum(x_{k}w_{kn})+b_{n})\)
\(\vec{y}=f(\vec{u})=(f(\sum_{k=0}^{m}(x_{k}w_{k1})+b_{1}), f(\sum(x_{k}w_{k2})+b_{2}), … , f(\sum(x_{k}w_{kn})+b_{n}))\)
入力\(\vec{x}\)、バイアス\(\vec{b}\)、重みW（重みはm×nのため行列になる）は以下のようにあらわせる。
\(\vec{x}=(x_{1},x_{2},…,x_{m})\)
\(\vec{b}=(b_{1},b_{2},…,b_{n})\)
\(W=\left(\begin{array}{cccc}w_{11}& w_{12}& …& w_{1n}\\w_{21}& w_{22}& …& w_{2n}\\…& …& …& …\\w_{m1}& w_{m2}& …& w_{mn}\end{array}\right)\)
※行に入力数、列にニューロン数。（1つのニューロンにm個の入力があるということ）

ちなみにuの計算をPythonで記述すると以下になる。
u = np.dot(x, w) + b

２．問題

ニューラルネットワークで解決する題目を問題という。
大きく２種類に分かれる。

種類	内容	出力数
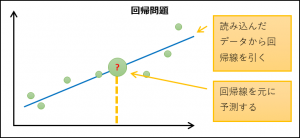
回帰問題	連続的な数値を予測する	1つ
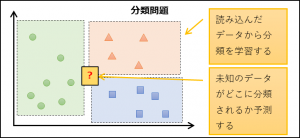
分類問題	分類分けを行う	分類する数

３．活性化関数

※関数自体の説明のため、入力はx、出力はyであらわしているが、実際の入力は活性化関数入力値なのでxでなくuの方がわかりやすいかもしれない。

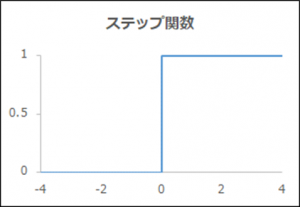
関数名「ステップ関数」

概要	0か1
出力y	0 (x≦0)、1 (x>0)
導関数y’	0
メリット、デメリット	実装が簡単だが、0と1の中間が表現できない。微分できないので、ニューラルネットワークでは使用できない

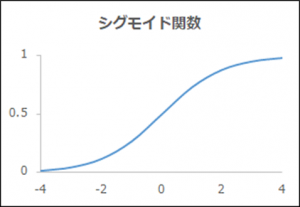
関数名「シグモイド関数」

概要	0と1の間を滑らかに変化
出力y	\(\frac{1}{1+exp(-x)}\)
導関数y’	\((1-y)y\)
メリット、デメリット	微分が扱いやすい（＝ニューラルネットワークで実装しやすい）

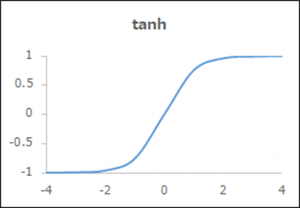
関数名「tanh」

概要	-1と1の間を滑らかに変化
出力y	\(\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}\)
導関数y’	\(\frac{4}{(exp(x)+exp(-x))^{2}}\)
メリット、デメリット	0を中心とし、バランスがいい

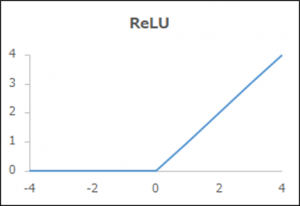
関数名「ReLU（ランプ関数）」

pic.

概要	正のみy=x
出力y	0 (x≦0)、x (x>0)
導関数y’	0 (x≦0)、1 (x>0)
メリット、デメリット	シンプルで層が多くなっても安定した学習が可能

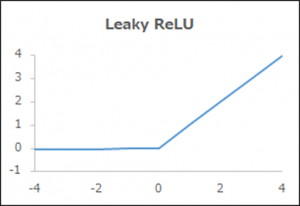
関数名「Leaky ReLU」

概要	ReLUが負でもわずかに変化
出力y	0.01x (x≦0)、x (x>0)
導関数y’	0.01 (x≦0)、1 (x>0)
メリット、デメリット	負でも学習が進む

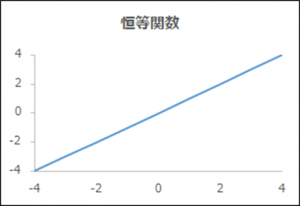
関数名「恒等関数」

概要	そのまま返す
出力y	x
導関数y’	1
メリット、デメリット	制限のない連続値のため回帰問題に適している

関数名「ソフトマックス関数」

概要	出力の合計が1
出力y	\(\frac{exp(x)}{\sum_{k=1}^{ニューロン数}exp(x_{k})}\)
導関数y’	\(exp(x)\)
メリット、デメリット	出力が0～1で合計が1なので分類問題に適している