 前から興味があったのです。
前から興味があったのです。
なぜ「AI入門」ではなく、「ディープラーニング入門」なのかというと手に取った本がたまたま「はじめてのディープラーニング(我妻幸長[著])」だったというだけ。たまたま手にした本だったけどわかりやすかった。微分も完全に忘れてたけど、それとなく分かった気にはなった。
基本的にはPythonコマンドや微分公式などの要点と自分なりにかみ砕いた説明を書いていくことにする。
最初はPythonというかNumpy(読みは「ナンパイ」でいいみたい)。
1.Numpyの関数
●shape
| shape(<numpy配列>) | 次元別要素数取得 |
import numpy as np
ary = np.array([ [ [0],[1] ],[ [2],[3] ],[ [4],[5] ] ])
print(np.shape(ary)) # 結果「(3, 2, 1)」
print(ary.shape) # numpy配列に対する処理はnumpy配列のメソッドとしても実行可能●size
| size(<numpy配列>) | 全要素数取得 |
print(np.size(ary)) # 結果「6」
print(len(ary)) # 結果「3」※最初の次元の要素数を返す
●zeros
| zeros(<要素数>) | 値が0の配列を作成 |
| zeros(<次元別要素数タプル>) | 値が0の多次元配列を作成 |
print(np.zeros(5)) # 結果「[0. 0. 0. 0. 0.]」
print(np.zeros((3,2,1))) # 0次元は3要素、1次元は2要素、3次元は1要素
●ones
| ones(<要素数>) | 値が1の配列を作成 |
| ones(<次元別要素数タプル>) | 値が1の多次元配列を作成 |
print(np.ones(5)) # 結果「[1. 1. 1. 1. 1.]」
print(np.ones((3,2,1))) # 0次元は3要素、1次元は2要素、3次元は1要素
●random
| random.rand(<要素数>) | 乱数の配列を作成 |
print(np.random.rand(5)) # 結果「[0.29067142 0.74922734 0.43699554 0.51483667 0.35425807]」
●arange
| arange(<開始値>,<終了値>,<間隔>) | 連続値の配列を作成 ※開始値省略時=0 ※間隔省略時=1 |
print(np.arange(-1, 1, 0.5)) # 結果「[-1. -0.5 0. 0.5]」
print(np.arange(3)) # 結果「[0 1 2]」
●linspace
| linspace(<開始値>,<終了値>,<要素数>) | 連続値の配列を作成 ※要素数省略時=50 |
print(np.linspace(-1, 1, 5)) # 結果「[-1. -0.5 0. 0.5 1. ]」
print(np.linspace(-25, 24)) # 結果「[-25. -24. ~ 23. 24.]」
●reshape
| reshape(<numpy配列>, <次元別要素数タプル>) | 形状変更 ※次元別要素数タプルに-1を指定すると、自動で判定する。-1のみだと1次元配列になる。途中で-1だと残りを自動計算する。 |
ary = np.array([i for i in range(6)])
print(np.reshape(ary, (2,3))) # 結果「[ [0,1,2],[3,4,5] ]」
print(np.reshape(ary, (2,3)).reshape(3,2)) # 結果「[ [0,1],[2,3],[4,5] ]」
print(np.reshape(ary, (2,3)).reshape(3,2).reshape(-1)) # 結果「[0 1 2 3 4 5]」※1次元配列に変換
print(np.reshape(ary, (2,3)).reshape(3,-1)) # 結果「[ [0,1],[2,3],[4,5] ]」
●sum
| sum(<numpy配列>) | 要素値合計 ※axisオプションで指定軸方向の合計 ※axisオプションと一緒にkeepdimsオプションを使用すると次元数をキープする |
a = np.array([ [1,2],[3,4] ])
print(np.sum(a)) # 結果「10」
print(np.sum(a, axis=0)) # 結果「[4,6]」
print(np.sum(a, axis=1)) # 結果「[3,7]」※次元数が減っていることに注意
print(np.sum(a, axis=1, keepdims=True)) # 結果「[ [3],[7] ]」
●max
| max(<numpy配列>) | 最大値取得 ※axisオプションで指定軸方向の最大値 ※sumと同様にkeepdimsオプションあり |
a = np.array([ [1,2],[3,4] ])
print(np.max(a)) # 結果「4」
print(np.max(a, axis=0)) # 結果「[3,4]」
print(np.max(a, axis=1)) # 結果「[2,4]」※次元数が減っていることに注意
print(np.max(a, axis=1, keepdims=True)) # 結果「[ [2],[4] ]」
●argmax
| argmax(<numpy配列>) | 最大値のインデックス取得 ※axisオプションで指定軸方向の最大値idx ※keepdimsオプションはない |
a = np.array([ [1,2],[4,3] ])
print(np.argmax(a)) # 結果「2」※1次元配列に形状変更した場合のインデックス
print(np.argmax(a, axis=0)) # 結果「[1,1]」
print(np.argmax(a, axis=1)) # 結果「[1,0]」※次元数が減っていることに注意
●where
| where(<numpy配列に対する条件>,<真値>,<偽値>) | 条件付き値変更 ※形状は条件に使用した配列と同じになる |
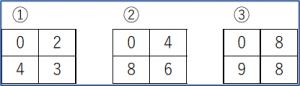
a = np.array([ [1,2],[4,3] ])
b = np.array([9,8])
print(np.where(a<2, 0, a)) # ①
print(np.where(a<2, 0, a*2)) # ②
print(np.where(a<2, 0, b)) # ③、aは形状のみに使用し、値はb(ブロードキャストできないとエラーになる)
2.numpy配列の演算
3.numpy配列の操作
(1) 要素抽出
a=np.array(["a","b","c"])
b=np.array([ ["a","b","c"],["d","e","f"] ])
print(a[1]) # "b"
print(b[1,2]) # "f"
# 以下はインデックスを複数指定している(単独の場合は数値でいいが、複数指定の場合はnumpy配列を渡す)
# 以下は1次元のidx=0,1、2次元のidx=2を指定しているので結果は「["c","f"]」となる
print(b[np.array([0,1]), np.array([2])])
# 以下のようにすると(0,2)と(1,1)のインデックスを指定することになるので、結果は「["c","e"]」となる
print(b[np.array([0,1]), np.array([2, 1])])
(2) 要素値変更
a[1] = "z"
b[1,2] = "y"
(3) 配列の取得
b2 = b[0] # 多次元配列を途中指定(bの0次元でidx=0を全部→["a","b","c"])
(4) 配列の置換
b[0] = ["g","h","i"] # 配列全置換(b→[ ["g","h","i"],["d","e","f"] ])
(5) スライシング(部分参照)
print(np.array([i for i in range(10)][1:3])) # 結果「[1 2]」

print(np.array([i for i in range(10)][::3])) # 結果「[0 3 6 9]」
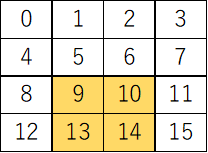
print(np.array([i for i in range(16)]).reshape(4,4)[2:, 1:3]) # 結果「[ [9,10],[13,14] ]」
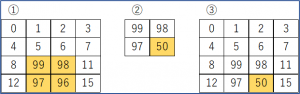
a=np.array([i for i in range(16)]).reshape(4,4)
a[2:, 1:3] = np.array([ [99,98],[97,96] ])
print(a) # ①
b = a[2:, 1:3]
b[1,1] = 50
print(b) # ②
print(a) # ③ ※bの入れ替えの影響を受けていることに注意。切り出してもメモリアドレスは同じ(シャローコピー)。
(6) 軸(axis)の入れ替え
a = np.array([i for i in range(6)]).reshape(3,2)
print(a)
"""結果
[0, 1],
[2, 3],
[4, 5]
"""
print(a.transpose(1,0)) # transpose(<1次元にする軸番号>、<2次元にする軸番号>)
"""結果
[ [0,2,4],
[1,3,5] ]
"""
print(a.T) # 「転置」結果はtranspose(1,0)と同じ
# 3次元の軸入れ替え
a = np.array([i for i in range(12)]).reshape(2,3,2)
print(a)
"""結果
[ [ 0, 1],
[ 2, 3],
[ 4, 5] ],
[ [ 6, 7],
[ 8, 9],
[10,11] ]
"""
print(a.transpose(1,0,2))
"""結果
[
[ [ 0, 1],
[ 6, 7] ],
[ [ 2, 3],
[ 8, 9] ],
[ [ 4, 5],
[10,11] ]
]
'"""
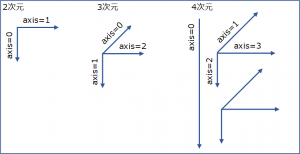
※「転置について」以下の通り、軸の順番を逆順に変更する
・2次元の場合・・・transpose(1,0)と同じ
・3次元の場合・・・transpose(2,1,0)と同じ
・4次元の場合・・・transpose(3,2,1,0)と同じ

