ちゃんと使っている所あるのだろうか？
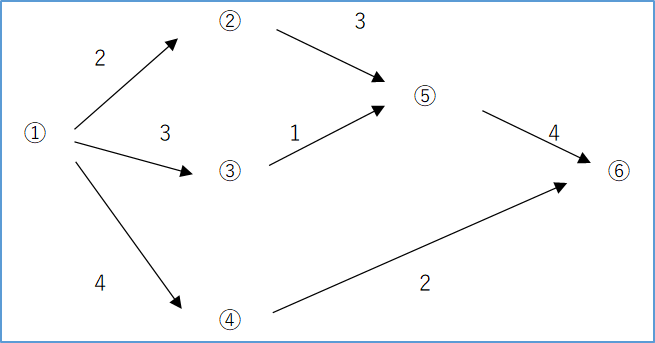
アローダイヤグラム
複数の工程が並んで進むようなプロジェクトを管理するのに適した日程管理手法。
(1) 作成手順
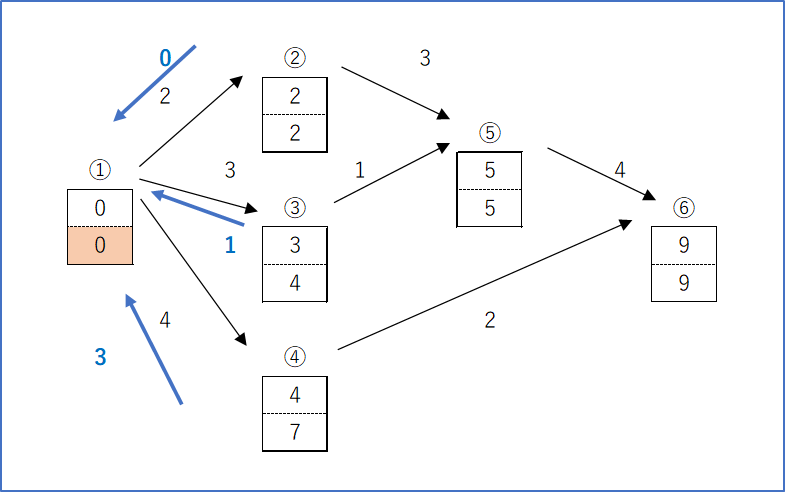
分析の為に最早結合点時刻（いつ始められるか）と最遅結合点時刻（いつ始めなければならないか）を求める。
<手順1>最早結合点時刻は最初の工程から順に計算する（前進計算）
※経路の最初は必ず0（図の①）
※複数経路が存在する場合、大きい方をとる。（図の⑤は「②経由の経路」の方が大きい）
<手順2>最遅結合点時刻は最後の工程から順に計算する（後進計算）
※経路の最後は必ず最早結合点時刻と同じ（図の⑥）
※複数経路が存在する場合、小さい方をとる。（図の①）
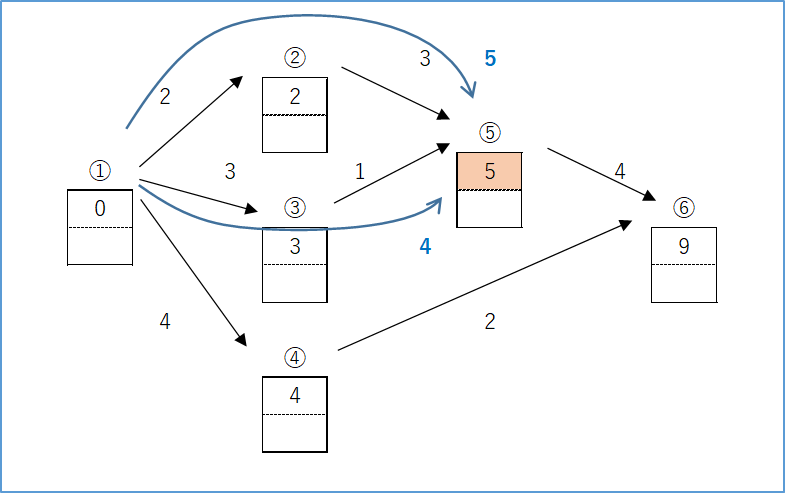
(2) クリティカルパス
最早結合点時刻と最遅結合点時刻で差がない結合点の経路。余裕がないということ。
(3) 短縮アプローチ
最早結合点時刻と最遅結合点時刻で差がある（余裕がある）結合点の経路を短縮しても全体の短縮につながらない。
※ダミー作業
上記では使用していないが、ダミー作業を示すことがある。点線矢印で表し工数０日の作業。工程順序はあるので、ダミー作業があることで待ちが発生することがある。
線形計画
制約のある中で最大効果を求める際に使用される手法
例えば、
●制約条件
4x + 8y <= 40
9x + 6y <= 54
●目的
「z = 2x +3y」においてzが最大となるx, yを求める
※xの売値2円、yの売値3円
制約条件1は在庫40個、xを作るのに4個使用する、yを作るのに8個使用する。
制約条件2は在庫54個、xを作るのに9個使用する、yを作るのに6個使用する。
というような状況。
●解く手順
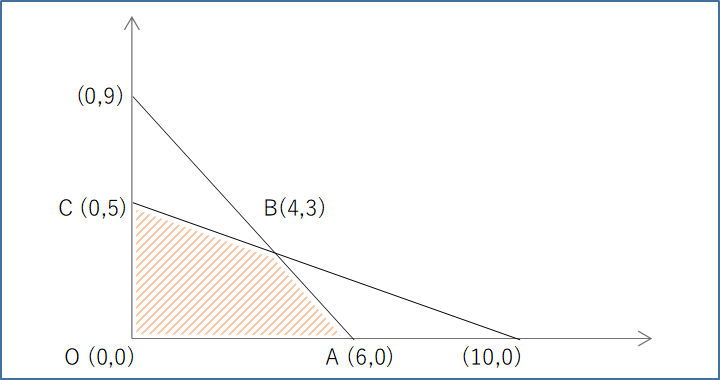
①制約条件でグラフ作成
※Bは制約条件の2次方程式で求まる
※制約条件を満たす範囲はOABCで囲まれた範囲内となる
②求めるx, y は範囲極大値なのでＡ, B, Cのいずれかになる。
それぞれの場合のzを求める
A：z = 2*6 + 3*0 = 12
B：z = 2*4 + 3*3 = 17
C：z = 2*0 + 3*5 = 15
以上から最大の組み合わせはＢのx=4, y=3 となる。