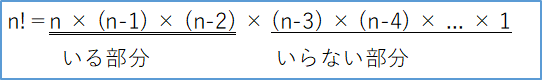学生時代に結局わからなかったとこ
※はじめに※ 自分が覚えやすい考え方を記載しています。考え方が正しいかは不明。公式はあってます。
一般的に
「順列（パームテーション）」は抽出する順番を考慮するパターン。
５つのボタンがあって押す順番で結果が変わるみたいなもの。
「組み合わせ（コンビネーション）」は抽出する順番を考慮しないパターン。
順番は関係なく、どのボタンを押したのか？等、結果のみ。条件に順番は含まれない。
順列
公式：nPr＝n!/(n-r)!
まず全抽出を考える。
抽出の度に選択肢が減っていくのを表すと「n → n-1 → n-2 → … → 1」となる。
順列の解となるパターン数は「n × (n-1) × (n-2) × … × 1」となるので、n!となる。
抽出回数rを考える。
2回抽出する場合は「n → n-1」で終わり。
3回抽出する場合は「n → n-1 → n-2」ここまで。
順列の解となるパターン数は2回抽出する場合「n × (n-1)」、3回抽出する場合「n × (n-1) × (n-2)」となる。
つまり順列とは「選択肢の階乗を頭から抽出回数分で止めた値」のこと。
公式で「抽出回数分で止める」をどう表しているかを考える。
3回抽出の場合、n!の先頭から3つ目までが必要。
このうち、いらない部分は(n-3)!と表せる。
順列の解を「いる部分×いらない部分÷いらない部分」と表現すると、「n! ÷ (n-3)!」となり、
抽出回数をrで置き換えると「n! ÷ (n-r)!」となり、公式と一致する。
組み合わせ
公式：nCr＝nPr/r!＝n!/(n-r)!*r!
考え方は、順列のうち並び替えると同じになる組み合わせを排除する。と考える。
選択肢がa～eで、3回抽出する場合、順列は5P3＝60となる。
このうち、抽出した選択肢に同じ組み合わせがいくつあるかを考える。（例えば、abcとcbaは同じ組み合わせ）
この同じ組み合わせ数をXとすれば、最終的に60/Xが組み合わせの解となる。
仮に選択肢a, b, cを抽出した場合の組み合わせは「abc, acd, bac, bca, cab, cba」の6個となり、これはすべて同じ組合わせ。
この個数（組み合わせ数）はa, b, cの総当たり数なので、選択肢が3つの全抽出と考え3P3で表せる。
他の抽出パターン（a, b, c以外の組み合わせ）も同じなので、1つの抽出パターンには3P3の同じ組み合わせがあることになる。よってXは3P3となる。
なので、解は「5P3/X＝60/X＝60/3P3＝60/6＝10」となる。
汎用的に書くと「nPr/rPr＝nPr/r!＝n!/(n-r)!*r!」となり、公式と一致する。