基本情報技術者試験に向けての情報処理基礎学習。最初は基数変換
基数変換
※お約束・・・10進数の数字は(99)10、2進数の数字だと(10)2と表記します。
（１） 10進数への変換
桁位置と対応する数にその桁の値を掛ける。
◇桁位置対応表
①２進数
②16進数
e.g.
(00110)2 → 24×0 + 23×0+ 22×1+ 21×1+ 20×0 = 6
2進数だと’2’で繰り上がるのだから桁位置が進数の指数になると考えるとわかりやすい。
例えば、3進数だと(10)3になるには(3)10必要。(20)3となるには同じ値を足せばいいので「(3)10×2」となる。
もう１回足す「(3)10×3＝(32)10」と、(30)3だが’3’で繰り上がるので(100)3となる。
このことから(10)3と(3)10が対応し、(100)3と(32)10が対応していることがわかる。
その上位の(1000)3は「(100)3×3＝(32)10×3＝(33)10」となり、順に指数が増えていくことがわかる。
※負のべき乗はイメージがわかなかったが、次のように考えるとわかりやすい。
指数が増えると「×2」が増えるということは、指数が減ると「×2」が減る。つまり「÷2」が増える。
なので、20から指数を1つ減らした2-1は20÷2と考えられる。
（２） 10進数からの変換
(a) 整数部
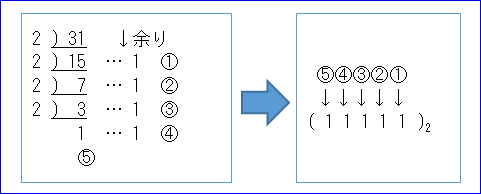
進数で割れなくなるまで割っていく。割った順番どおりに余りを並べるとその進数での表記になる。
※進数で繰り上がるのだから何回割れるかで桁数がわかると考える？
e.g.「(31)10を2進数に変換」
※最初の余りの’1’は単純に’1’の価値しかないが、次の余りの’1’は1回’2’で割った商に対する値なので2倍の価値がある。
そのため、最初に割った方の余りを下位桁として並べる。
(b) 小数部
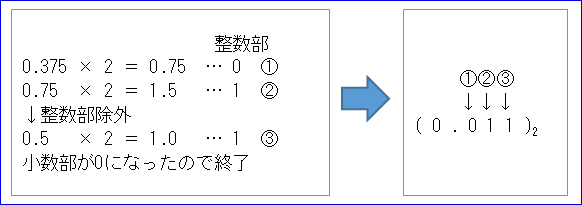
進数で小数部がなくなるまで掛けていく。繰り上がって整数になった部分は除外していく。
整数部を並べるとその進数での表記となる。
e.g.「(0.375)10を2進数に変換」
